Symmetrie is samen met periodiciteit de belangrijkste eigenschap van kristallen, zoals bijvoorbeeld dit sneeuwvlokje - dat wil zeggen, dit ijskristal. Het bestaat uit de onveranderlijkheid van kristallen (van hun morfologie of structuur) met betrekking tot bepaalde eenvoudige bewerkingen, zoals rotatie: als we dit ijskristal 60 graden draaien zonder dat je het weet, zou je het verschil niet kunnen onderscheiden.
Dit zou hetzelfde zijn als we het 120º, 180º, 240º, 300º of, blijkbaar, 360º draaien (een volledige omwenteling waardoor het kristal terugkeert naar zijn oorspronkelijke positie). We zeggen dat het kristal "draaisymmetrie van orde 6" of "zeshoekige symmetrie" heeft.

Naast rotatiesymmetrie is er ook reflectiesymmetrie (reflectie als in spiegels), inversiecentra, translatiesymmetrie en combinaties daarvan zoals schroefassen of glijvlakken.
Kristallografen houden van symmetrie, soms tot het punt van obsessie. We zijn symmetrie-freaks. Je zou kunnen denken dat wat ons aantrekt de schoonheid van kristallen en kristallijne structuren is, waarvan de harmonie zonder twijfel verbonden is met de symmetrie. Inderdaad, we vinden dit net zo mooi als de ontwerpers van het Alhambra, en zoals de Marokkaanse ambachtslieden dat nog steeds doen.

Maar bovenal houden we van symmetrie omdat het de studie van kristallijne structuren enorm vereenvoudigt. Zo komt de periodiciteit zelf voort uit een werking van symmetrie: de vertaling. Als we de cel-eenheid van een kristal een periodieke afstand vertalen, verandert de structuur niet: ze is invariant. Dit stelt ons in staat om een enorme kristallijne structuur weer te geven door de weinige atomen van zijn cel-eenheid, waarbij we het bijna oneindige aantal andere atomen in de structuur vergeten.

Translationele symmetrie stelt ons in staat om de immense kristalstructuur te kennen door alleen de atoomconfiguratie in de eenheidscel te bestuderen.
De andere symmetrieën van rotatie, reflectie en inversie verminderen de representatie nog meer omdat een deel van de atomen die zich in de eenheidscel bevinden symmetrische kopieën zijn van andere atomen in dezelfde cel.
Symmetrie maakt het leven van kristallografen eenvoudiger, waardoor het mogelijk is om kristallijne structuren te classificeren en te begrijpen. Hoeveel soorten kristal bestaan er? Dat wil zeggen, in hoeveel verschillende vormen kan de materie zich organiseren? Hoewel ze misschien grenzeloos lijken, zijn er eigenlijk maar weinig mogelijkheden om een ruimte op een geordende manier op te vullen door periodiek een zelfde stuk te herhalen.
Rasters
Er bestaan bijvoorbeeld maar vijf soorten rasters:Met andere woorden, als we een oppervlak willen vullen, kunnen we dat doen met rechthoeken, driehoeken, vierkanten of zeshoeken, maar niet met vijfhoeken. En het is ook zo dat bij kristallijne structuren de draaisymmetrie slechts van orde 1, 2, 3, 4 of 6 kan zijn. Dankzij de studie van de combinaties van symmetrie weten we dat er maar 17 verschillende vormen zijn die een oppervlak kunnen betegelen, vormen die al bekend waren bij de Arabische meetkundigen.
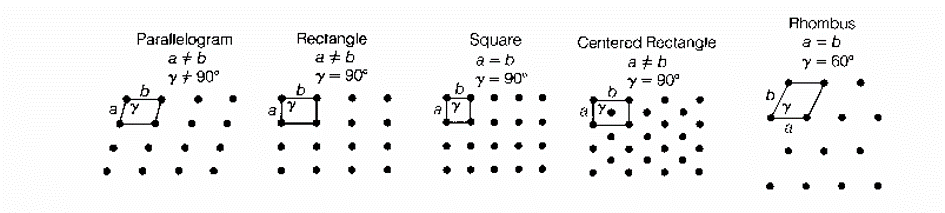
De Arabische ambachtslieden van de 18e eeuw kenden de 17 vlakke groepen van symmetrie. En het is ook aangetoond dat er slechts 230 verschillende vormen van periodiek verpakken van een volume met identieke eenheden zijn. Niet één meer, niet één minder.

QUASICRYSTALS
Moleculen kunnen draaisymmetrie 5 hebben - met andere woorden, als ze 72º draaien zijn ze invariant. Maar het is onmogelijk om er een oppervlak mee te vullen, of een netwerk mee te maken; dat wil zeggen dat het onmogelijk is om er een kristal mee te bouwen. Daarom zul je geen vijfhoekige vloertegels te koop vinden; of als je dat wel doet, worden ze gecombineerd met de rhombi die nodig is om de onvermijdelijke gaten tussen de vijfhoeken op te vullen. Moleculen kunnen vijfhoekige symmetrie hebben, maar periodieke structuren niet.
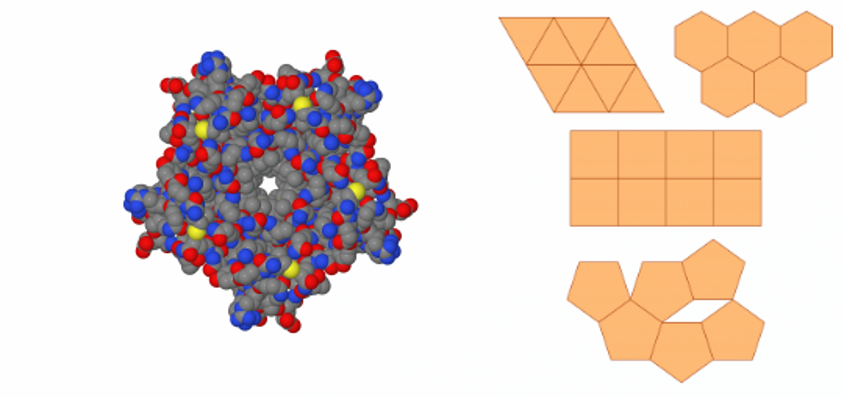
Het bestaan van kristallen met orde 5 symmetrie is echter recentelijk ontdekt.
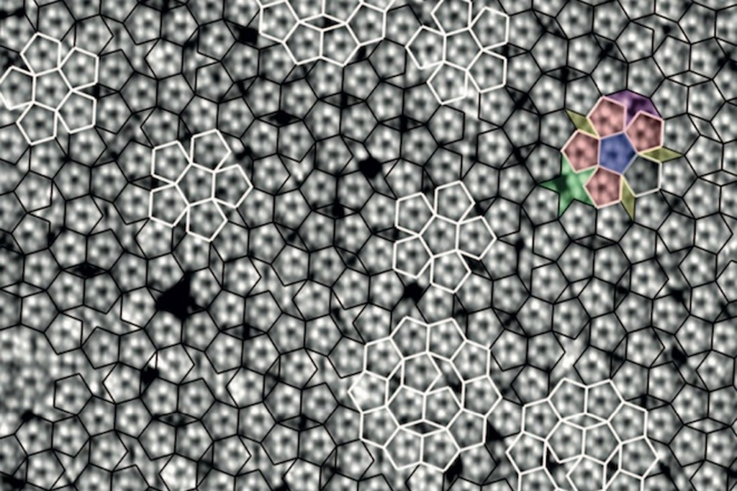
De verklaring ligt in het feit dat de oppervlakken en volumes volledig kunnen worden opgevuld volgens regelmatige, maar niet noodzakelijkerwijs periodiek perfecte, patronen. Dit kan bijvoorbeeld gebeuren met dilatatiesymmetrie, waarbij patronen zoals de volgorde van de Gulden Snede worden gevolgd. Met andere woorden, materialen die quasi-periodiek georganiseerd zijn. Het zijn de zogenaamde quasi-kristallen.

WIST U DAT...
Geen twee sneeuwvlokken zijn gelijk, want de groei van elk ijskristal is afhankelijk van meerdere factoren.
In 1891 toonde Fedorov aan dat er niet meer dan 17 basisstructuren zijn voor de oneindig mogelijke decoraties van het vlak gevormd door periodieke mozaïeken.
Symmetrie is een concept dat achter veel dingen schuilgaat: in de biologie bijvoorbeeld is het H1N1-virus een symmetrisch object en gebruikt het symmetrie om te repliceren.
De tegels van het Alhambra zijn gerangschikt in obsessieve plots en herhalingen, beheerst door een strikte reeks van symmetrische schema's, op zo'n manier dat als ze geroteerd worden ze hetzelfde uiterlijk behouden (vrij gelijkaardig aan het roteren van een gelijkzijdige driehoek), wat misschien iets van hun betoverende aantrekkingskracht verklaart.