Deze interactieve installatie biedt drie tafels met methacrylaatstukken voor het bouwen van tweedimensionale patronen die het mogelijk maken om te experimenteren met sleutelbegrippen van de kristallografie.

Kristallen worden gevormd door miljoenen kleine stukjes materie, of het nu gaat om atomen, moleculen of macromoleculen.
Deze kleine stukjes materie zijn als de stukjes van een grote puzzel, dat is het kristal.
Maar deze puzzel is anders.
In normale decoupeerzagen is elk stukje anders dan de rest en past het maar in één bepaalde positie. In kristallen zijn alle stukjes, dus alle moleculen, gelijk, wat betekent dat het doen van de kristallijne decoupeerzaag relatief eenvoudig is. Het is als een mozaïek waarvan de stukken - die in het Engels de mooie naam tesserae hebben - allemaal identiek zijn.
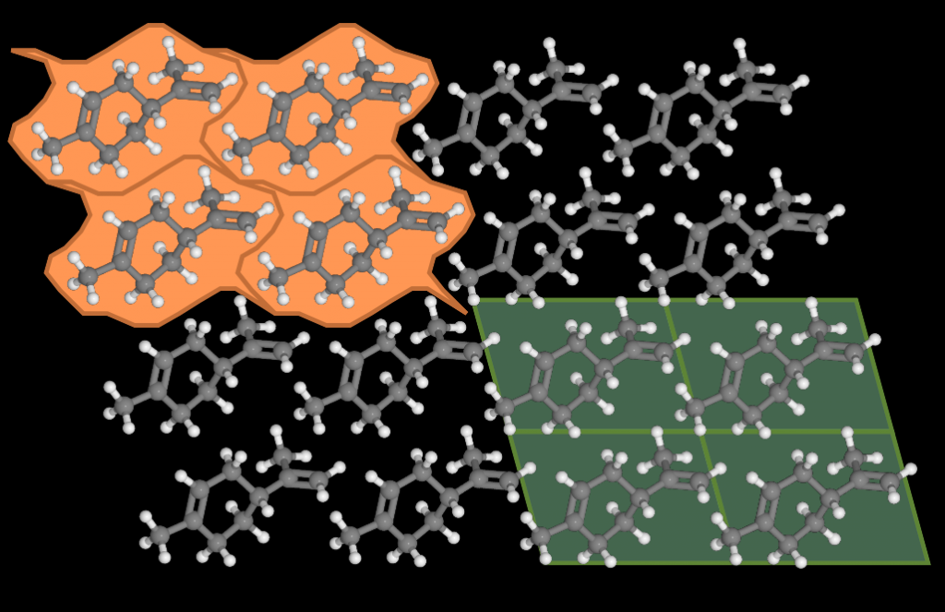
Hierboven is een kristallijne legpuzzel, een mozaïek. De tesserae, de moleculen van een kristal, zijn allemaal identiek maar hebben de neiging om complexe vormen te hebben (weergegeven in kleur oranje). Wij kristallografen zetten deze complexe vormen graag om in eenvoudiger geometrische vormen (in het groen) om de berekeningen eenvoudiger en de demonstraties eenvoudiger en eleganter te maken. Zo kan bijvoorbeeld worden aangetoond dat er slechts vijf verschillende soorten tesserae op een vlak zijn en veertien in de ruimte.
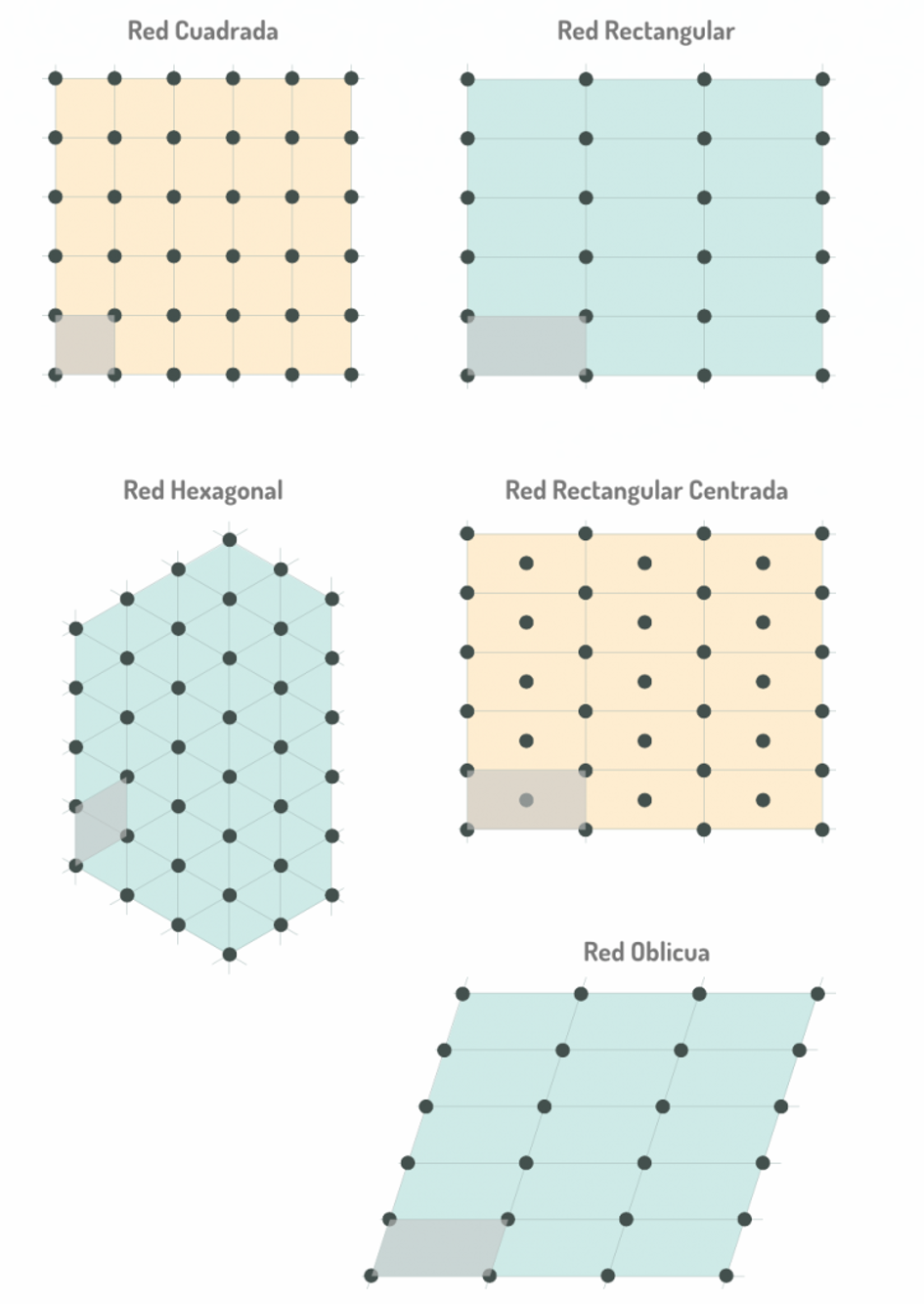
Boven de vijf tweedimensionale tesserae zijn geïllustreerd, die in de kristallografie "eenheidscellen" worden genoemd, de herhaalde elementen waarmee de vijf tweedimensionale roosters zijn opgebouwd - met andere woorden, de enige vijf mogelijke manieren om een vlak te vullen. Op de tabel vindt u de tesserae om de vijf soorten kristallijne mozaïeken te construeren.
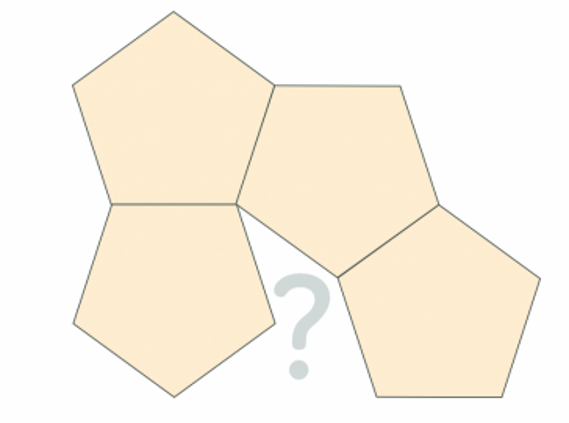
U zult gemerkt hebben dat de eenheidscellen driehoekige, vierkante, rechthoekige en zeshoekige stukken zijn. Waarom zijn er geen vijfhoeken? Waarom is er geen rooster dat de verpakking van vijfhoeken laat zien? Probeer het vliegtuig te bedekken met vijfhoeken en u zult ontdekken waarom...
In dit paneel kunnen we het verschil tussen een kristal, een quasikristal en amorf glas bekijken.
Maak het kristal met twee soorten tesserae. Ze kunnen hetzelfde of verschillend zijn. Maar ze moeten wel periodiek worden aangebracht - de afstand tussen de stukken van een zelfde type in dezelfde richting moet altijd hetzelfde zijn.
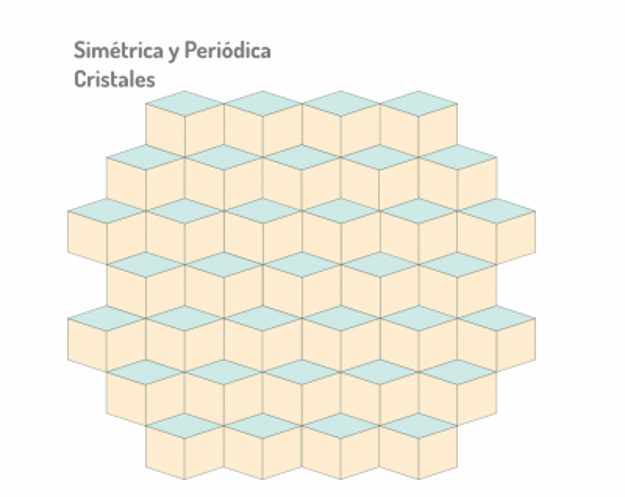
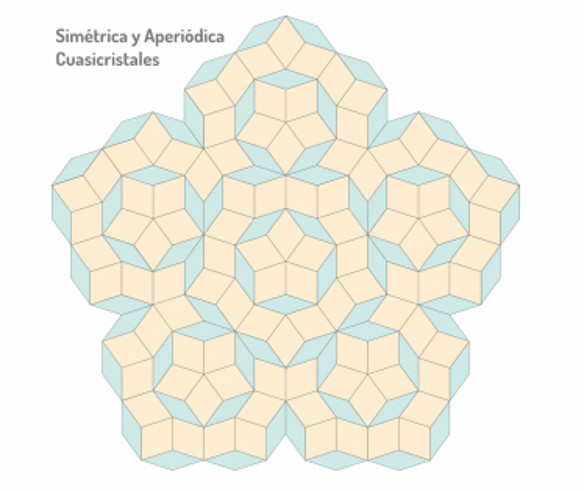
Als we dezelfde tesserae symmetrisch maar niet periodiek stapelen, bouwen we een quasikristal zoals hieronder.
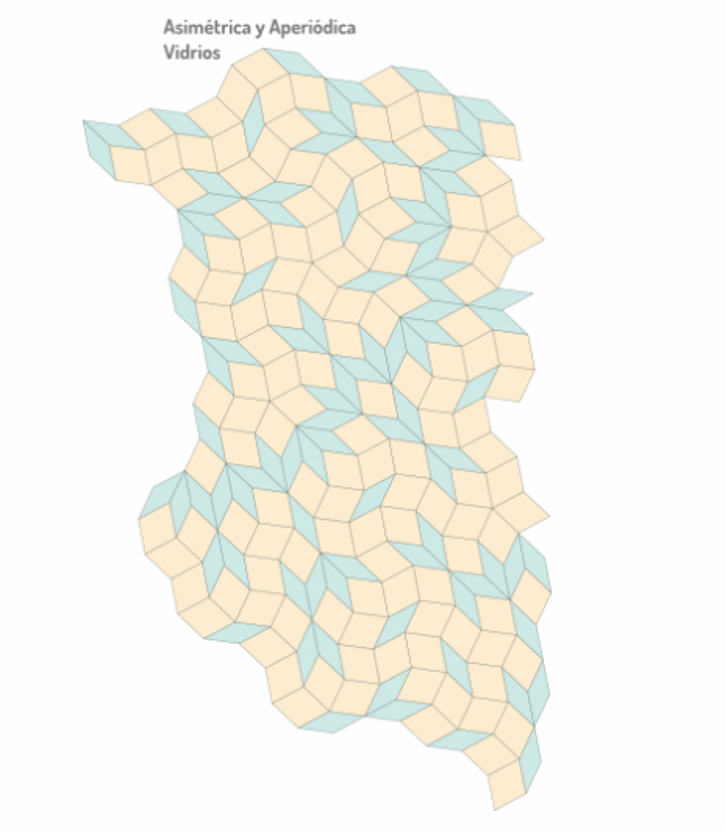
Als we ten slotte zowel de symmetrie als de periodiciteit afschaffen, is het resultaat een amorf patroon, zoals dit hieronder.
Hoewel er slechts vijf tweedimensionale roosters zijn, met verschillende soorten tesserae of verschillende oriëntaties van dezelfde tesserae, is het mogelijk om een grote verscheidenheid aan kristallografische patronen te bouwen.
Deze patronen zijn kristallografisch zolang ze de regels van symmetrie en periodiciteit respecteren die je ontdekt als je met de tesserae op tafel speelt.
Je hebt je waarschijnlijk afgevraagd: als er zoveel patronen kunnen zijn, hoe zit het dan met die slechts vijf roosters, die slechts vijf soorten eenheidscellen? Nou, je kunt zelf zien dat ze blijven werken. Probeer de herhaalde eenheid (de eenheidscel) te vinden in de patronen die je maakt. In de voorbeeldpatronen op dit paneel is de eenheid van de cel voor jou in het grijs weergegeven.
Als u meer wilt, bekijk dan de patronen aan de rechterkant. Naast de eenheidscel (in het grijs) is een tweede eenheidscel gemarkeerd (in het roze) die overeenkomt met de eenheidscel als we rekening houden met de kleuren van de stukken. Het identificeren van deze periodiciteit is geen sinecure, zelfs niet voor veel kristallografen. Gefeliciteerd als het je lukt.

karaf, whiskykaraf, whiskey karaf, kristallen karaf, wijnkaraffen, wijnkaraf, kristal karaf, decanteer karaf, whiskey karaf kristal, kristal karaf, glazen karaf, karaf graveren, champagneglazen, whisky glazen, whiskey glazen. bij Kristalglas.nl